Fixed Hydraulic Resistance —— Fixed Orifices

Hydraulic resistance, as a component that creates obstruction to fluid flow, can be divided into fixed hydraulic resistance and variable hydraulic resistance. Fixed hydraulic resistance refers to flow passages (components) whose opening shape and area remain essentially unchanged during operation. There are multiple forms of fixed hydraulic resistance in hydraulic technology; here we introduce only the most common types —— gaps, long thin holes, and thin-walled small holes.

1. Gaps

(1) Gaps between rectangular planar surfaces

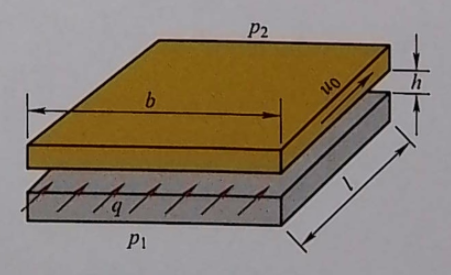
If two rectangular surfaces are parallel, the gap height is much smaller than the width and length, the oil viscosity is high, the pressure difference between the two sides is not large, and the flow rate is small, the flow state maintains laminar flow. When there is no relative motion between the two planes, the theoretical formula for the oil flow rate q through the gap is:

q = (b×h³×Δp)÷(12×ν×ρ×l)

Where:

• b —— gap width;
• h —— gap height;
• l —— gap length;
• Δp —— pressure difference (Δp = p₁ – p₂);
• ν —— oil kinematic viscosity;
• ρ —— oil density.

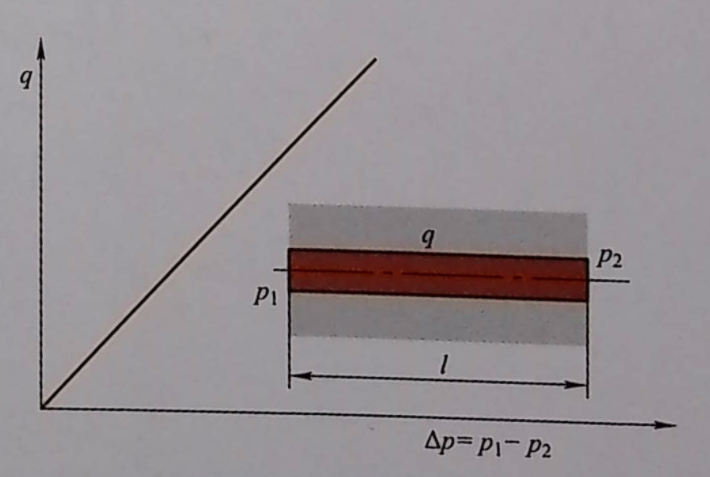
At this time, flow rate q is roughly proportional to pressure difference Δp and proportional to the cube of gap height. The hydraulic resistance can be written similar to Ohm’s law as:

Δp÷q = (12×ν×ρ×l)÷(b×h³)

If the two planes have relative motion, a relative motion term needs to be added to the flow rate:

q = (b×h³×Δp)÷(12×ν×ρ×l) + (b×h×u₀)÷2

Where u₀ —— relative movement velocity of the two surfaces. At this time, “hydraulic resistance = pressure difference / flow rate” can no longer be defined.

(2) Cylindrical annular gap

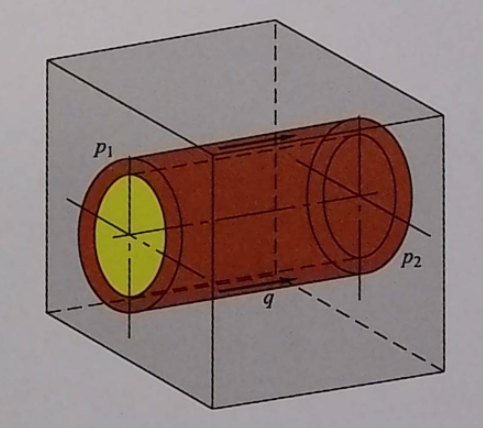
If the gap is cylindrical annular, the flow rate formula through this gap during laminar flow is:

q = (π×d×s³×Δp)÷(12×ν×ρ×l)

Where:

• d —— cylinder diameter;
• s —— gap height;
• Δp —— pressure difference (Δp = p₁ – p₂);
• ν —— oil kinematic viscosity;
• ρ —— oil density;
• l —— gap length.

Example: When cylinder diameter is 15mm, gap height is 0.01mm, length is 5mm, and pressure difference is 10MPa, the flow rate is approximately 1.4mL/min (can be calculated using “Hydraulic Valve Estimation 2023” software).

2. Long Thin Holes

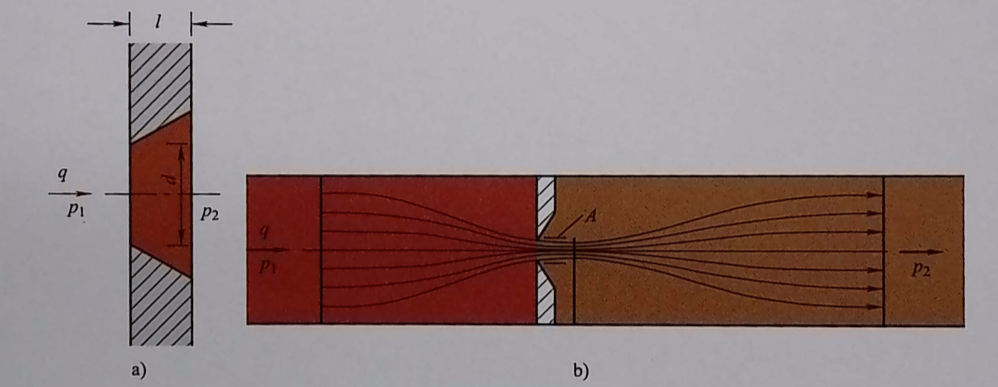
If a small hole is long and thin (hole length l is greater than 8 times the hole radius r), the pressure difference between the two sides is not large, and the flow state maintains laminar flow, the flow rate q has a linear relationship with the pressure difference Δp at both ends of the hole:

q = (π×r⁴×Δp)÷(8×ν×ρ×l)

Where:

• ν —— oil kinematic viscosity;
• ρ —— oil density;
• r —— hole radius;
• l —— hole length;
• Δp —— pressure difference (Δp = p₁ – p₂).

3. Thin-Walled Small Holes

If the small hole wall is very thin relative to the hole diameter, the pressure difference between the two sides is large, the flow velocity is high, and the flow state is turbulent, the fluid has little contact with the solid wall surface, and the flow rate q is basically unaffected by oil viscosity.

Thin-walled small hole flow rate formula:

q = α×A×√(2×Δp÷ρ)

Where:

• α —— flow coefficient related to hole shape;
• A —— hole area (A = π×d²÷4);
• Δp —— pressure difference (Δp = p₁ – p₂);
• ρ —— oil density.

The flow velocity at the small hole is usually very high: when Δp is 5MPa, the flow velocity is approximately 100m/s; when Δp is 10MPa, it is approximately 150m/s.

If the diameter of the passage before the hole exceeds 7 times the hole diameter and the hole wall thickness is less than the hole radius, the hole can be considered an ideal thin-walled hole, and α can be taken as 0.6.

Notes: 1) If the hole diameter equals the wall thickness and there is no chamfer, α is 0.72~0.77; with slight chamfering, α may reach 1 (larger flow rate under the same pressure difference). 2) If the flow direction is from large to small, α>2.

4. Actual Operating Conditions

Theoretical classification: wall thickness > 8 times hole radius (laminar flow) → calculate according to long thin hole; wall thickness < hole radius (turbulent flow) → calculate according to thin-walled hole. Intermediate cases (wall thickness between the two, non-circular flow passage, uncertain flow state): no theoretical formula, refer only to measurement data.

The pressure difference – flow rate relationship for thin sharp edges (thin-walled openings in valves, non-circular) is usually expressed as:

q = α×A×(2×Δp÷ρ)^m

Where m = 0.5 ~ 1.

For simplicity, the flow rate for all openings can be approximately expressed as:

q = k×A×√Δp (or q is proportional to A×√Δp)

Where:

• k —— comprehensive constant containing flow coefficient and oil density;
• A —— opening area;
• Δp —— pressure difference.

This relationship is a quadratic parabola: the larger the pressure difference, the larger the flow rate; the smaller the opening area and the larger the flow rate, the larger the pressure difference.

Theoretically, when the pressure difference is large enough, the flow rate can be arbitrarily large, but the pressure loss increases quadratically; when large flow rate and small pressure loss are needed, the opening area should be increased.

5. Small Holes in Series

When two small holes are connected in series, the proportion of pressure drop Δp₁ of hole 1 to the total pressure drop Δp is:

Δp₁÷Δp = d₂⁴÷(d₁⁴ + d₂⁴)

(Pressure drop is inversely proportional to the 4th power of hole diameter)

Example (hole 2 diameter = 1):

• Hole 1 diameter = 1: pressure drops are the same for both;
• Hole 1 diameter = 0.5: hole 1 pressure drop accounts for 94%;
• Hole 1 diameter = 0.3: hole 1 pressure drop accounts for 99.2%.

The minimum flow cross-section (small hole) in the flow passage accounts for the main pressure drop and requires focused attention.