Menu
Section 2: Fundamentals of Hydrostatics and Hydraulic Pressure
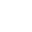
Hydrostatics is the branch of fluid mechanics that studies the mechanical properties of liquids at rest. The term "at rest" refers to a state where there is no relative motion between the liquid particles themselves. Whether the container holding the liquid is stationary or in motion is irrelevant to the hydrostatic analysis, as long as the liquid maintains its internal equilibrium state.
Hydrostatic principles govern the behavior of liquids at rest, with applications in various engineering systems
1. Understanding Hydraulic Pressure in Liquid Systems
The force per unit area acting perpendicular to a surface in a liquid is defined as hydraulic pressure. While this concept is technically referred to as "pressure intensity" in physics, it is conventionally called pressure in hydraulic transmission systems. Hydraulic pressure is typically denoted by the symbol p. When a normal force ΔF acts on a liquid surface area ΔA, the hydraulic pressure at any point within the liquid can be expressed mathematically as:
p = lim(ΔA→0) ΔF/ΔA
Characteristics of Hydraulic Pressure
- Hydraulic pressure always acts perpendicular to the surface, directed along the inward normal to the pressure-bearing surface.
- In a static liquid, the hydraulic pressure at any given point is equal in all directions, demonstrating the isotropic nature of pressure in fluids at rest.
These properties indicate that static liquids are always in a state of compression, with every particle within the liquid experiencing balanced pressure forces from all directions. This equilibrium state is fundamental to understanding how hydraulic pressure behaves in practical applications.
2. Distribution of Hydraulic Pressure in Static Liquids Under Gravity
Consider a container filled with liquid of density ρ in a static state, as illustrated in typical hydraulic systems. To determine the hydraulic pressure p at any arbitrary depth h below the liquid surface, we can analyze a vertical column of liquid extending from the surface downward.
Since the liquid column is in equilibrium, the force balance equation yields:
pΔA = p₀ΔA + ρghΔA
Simplifying this equation, we obtain:
p = p₀ + ρgh
This expression is known as the fundamental equation of hydrostatics (Equation 2-14).
Pressure distribution in a static liquid column
From this relationship, we can identify several key characteristics of hydraulic pressure distribution in static liquids under gravitational influence:
1. The hydraulic pressure at any point within a static liquid consists of two components: the pressure p₀ acting on the liquid surface, and the pressure contribution from the weight of the liquid column above that point, expressed as the product ρgh where h is the depth below the surface.
2. When the liquid surface is exposed only to atmospheric pressure pₐ, the hydraulic pressure at any point becomes:
p = pₐ + ρgh
3. The hydraulic pressure in a static liquid varies linearly with depth, following a straight-line distribution pattern.
4. Points at equal distances from the liquid surface form isobaric surfaces (surfaces of constant pressure), which are horizontal planes in the gravitational field.
3. Methods of Expressing and Measuring Hydraulic Pressure
Hydraulic pressure can be expressed using different reference points, leading to two primary measurement systems: absolute pressure and relative pressure (gauge pressure).

Various instruments are used to measure hydraulic pressure in different applications
Absolute Pressure
Absolute pressure is measured with respect to a perfect vacuum as the reference point. The pressure p expressed in Equation (2-15) represents absolute pressure, as it includes all pressure contributions acting on the liquid.
Relative Pressure (Gauge Pressure)
The portion of hydraulic pressure that exceeds atmospheric pressure, expressed as (p - pₐ = ρgh), is measured relative to atmospheric pressure pₐ as the reference. This is called relative pressure or gauge pressure. On Earth's surface, all objects are surrounded by the atmosphere, and atmospheric pressure acts uniformly on all surfaces. Consequently, pressure gauges read zero when exposed to atmospheric conditions, and their measurements represent relative pressure values. In hydraulic technology and engineering applications, unless specifically stated otherwise, hydraulic pressure typically refers to gauge pressure.
Vacuum Pressure
When the absolute pressure at a point in a liquid falls below atmospheric pressure, the difference below atmospheric pressure is termed vacuum pressure or vacuum degree. Using atmospheric pressure as the reference baseline, positive values above this baseline represent gauge pressure, while negative values below indicate vacuum pressure. For example, if the absolute pressure at a point in a liquid is 0.3×10⁵ Pa, its relative pressure would be:
p - pₐ = (0.3×10⁵ - 1×10⁵) Pa = -0.7×10⁵ Pa
This indicates a vacuum pressure of 0.7×10⁵ Pa (assuming pₐ ≈ 1×10⁵ Pa).
Units of Hydraulic Pressure
Common units for expressing hydraulic pressure include:
- Pa (Pascal, N/m²)
- MPa (Megapascal, N/mm²)
- bar (although not an SI unit, still used in some applications)
The conversion relationships between these units are:
- 1 MPa = 10⁶ Pa
- 1 bar = 10⁵ Pa
4. Example Application of Hydraulic Pressure Calculation
Example 2-1:
Consider a container filled with oil, where the oil density ρ = 900 kg/m³. A piston with area A = 1×10⁻³ m² is subjected to a force F = 1000 N. Assuming the piston weight is negligible, calculate the hydraulic pressure at a depth h = 0.5 m below the piston.
Solution:
The hydraulic pressure at the piston-liquid interface is:
p₀ = F/A = 1000/(1×10⁻³) N/m² = 10⁶ N/m²
Using the hydrostatic equation (2-14), the hydraulic pressure at depth h is:
p = p₀ + ρgh = 10⁶ + 900×9.8×0.5 N/m²
p = 1.0044×10⁶ N/m² ≈ 10⁶ N/m² = 10⁶ Pa
This example demonstrates an important principle in hydraulic systems: the pressure contribution from liquid weight (ρgh) is often negligible compared to externally applied hydraulic pressure. Therefore, in analyzing hydraulic systems, we can approximate that hydraulic pressure is uniform throughout the liquid volume, simplifying many practical calculations.
5. Pascal's Principle and Transmission of Hydraulic Pressure
In a closed container containing static liquid, as shown in typical hydraulic systems, when an external force F causes a change in the applied pressure p₀, the liquid maintains its static equilibrium state. Under these conditions, any change in hydraulic pressure at one point is transmitted equally to all points within the liquid. This fundamental principle is known as Pascal's Law or the principle of hydraulic pressure transmission.
According to Pascal's principle, in a closed container system, hydraulic pressure applied to a static liquid is transmitted undiminished and equally in all directions throughout the liquid. This relationship maintains a direct proportionality between the hydraulic pressure p in the container and the applied load F:
p = F/A
where A represents the cross-sectional area of the piston or pressure-applying surface.
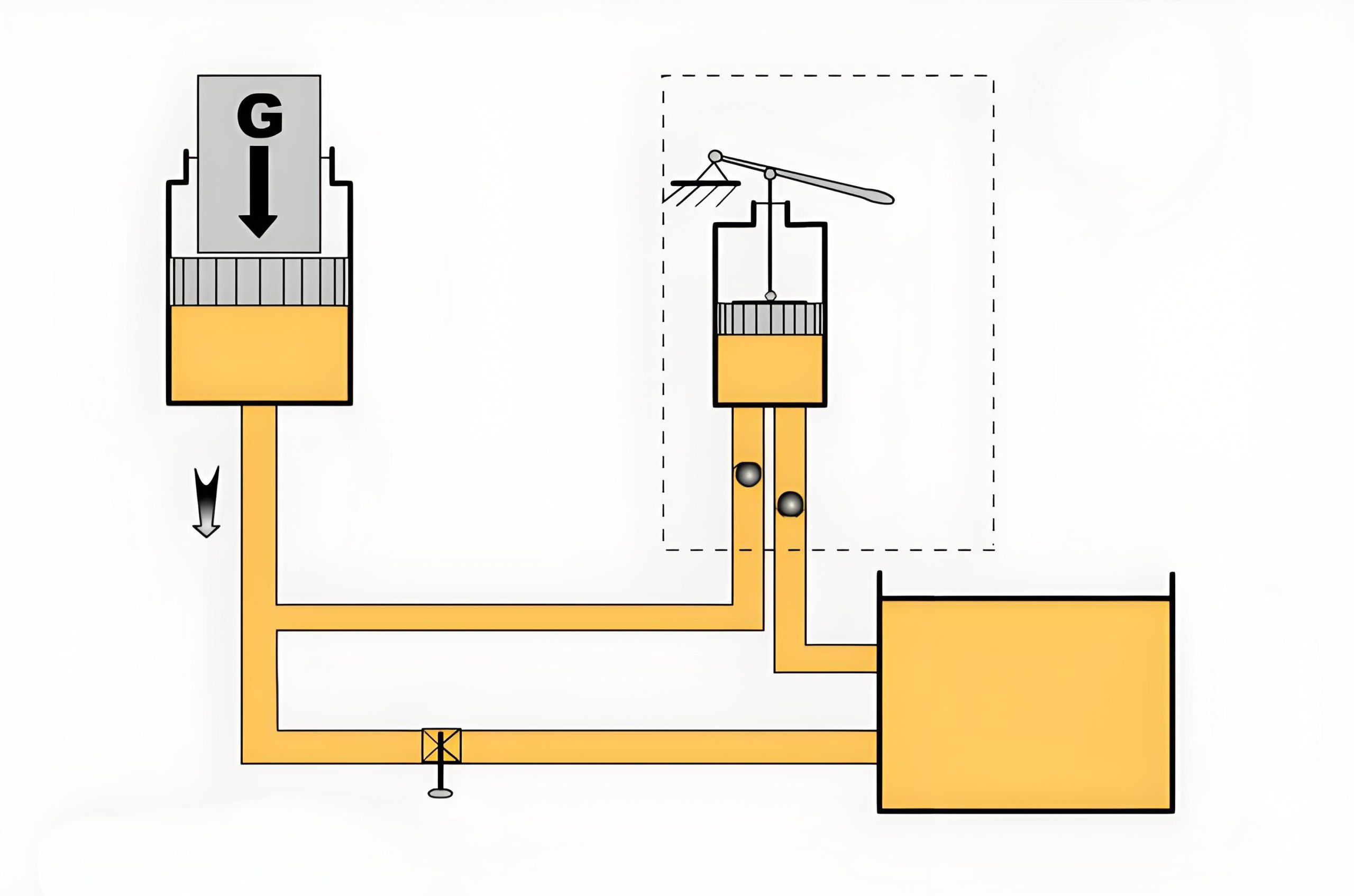
This principle forms the theoretical foundation for numerous hydraulic applications, including hydraulic presses, hydraulic jacks, hydraulic brakes, and various hydraulic transmission systems used in industrial machinery and vehicles.
6. Forces Exerted by Hydraulic Pressure on Solid Surfaces
In hydraulic transmission systems, since the pressure contribution from liquid weight is typically neglected, the static hydraulic pressure can be considered uniformly distributed throughout the liquid volume. When liquid contacts solid surfaces, these surfaces experience forces due to hydraulic pressure.
Forces on Plane Surfaces
For a flat solid surface in contact with liquid, the total force F exerted by the static liquid equals the product of hydraulic pressure p and the surface area A. The force direction is perpendicular to the surface:
F = pA
This straightforward relationship makes it easy to calculate forces on pistons, valve seats, and other flat components in hydraulic systems.
Forces on Curved Surfaces
When dealing with curved surfaces, the direction of hydraulic pressure varies across the surface, though its magnitude remains constant at a given depth. Consider a hydraulic cylinder with internal radius r and length l.
The force exerted by hydraulic pressure on a curved surface in any given direction equals the product of the liquid pressure and the projected area of the surface in that direction.
Mathematical Derivation for Curved Surfaces:
Taking a small area element dA = lds = lr dθ on the internal surface (where θ is the angular position), the horizontal component of the force dF acting on this element due to hydraulic pressure is:
dFₓ = dF cos θ = p dA cos θ = plr cos θ dθ
Integrating over the right half of the cylinder (from -π/2 to π/2):
Fₓ = ∫₍₋π/₂₎^(π/2) dFₓ = ∫₍₋π/₂₎^(π/2) plr cos θ dθ = 2plr = pAₓ
where Aₓ = 2rl represents the projected area of the right half of the internal surface in the x-direction.
This result reveals an important principle that significantly simplifies force calculations for complex geometries in hydraulic components.
7. Advanced Applications of Hydraulic Pressure Principles
The fundamental principles of hydraulic pressure find extensive applications in modern engineering and technology. Understanding how hydraulic pressure behaves in static conditions provides the foundation for designing efficient hydraulic systems.
Pressure Intensification
By applying Pascal's principle with pistons of different areas, hydraulic systems can achieve pressure intensification. A small force applied to a small piston can generate much larger forces on a larger piston.
Pressure Distribution
In real hydraulic systems, components often have complex shapes. The principle that hydraulic pressure acts perpendicular to surfaces simplifies design and analysis of these components.
Energy Storage
Hydraulic pressure serves as an efficient means of storing and transmitting energy. Accumulators store energy by compressing gas or springs against hydraulic pressure.
8. Practical Considerations in Hydraulic Pressure Systems
When implementing hydraulic systems, several practical factors must be considered beyond the theoretical principles:
Temperature Effects
Temperature variations affect liquid density and viscosity, which can influence hydraulic pressure behavior. While the basic hydrostatic principles remain valid, temperature compensation may be necessary in precision applications.
Dynamic Effects
Although hydrostatics deals with liquids at rest, real systems often involve moving liquids. The transition from static to dynamic conditions introduces additional pressure components due to fluid acceleration and friction losses.
Safety Factors
Hydraulic systems often operate at high pressures, requiring careful attention to safety. Components must be designed with appropriate safety factors to withstand maximum hydraulic pressure plus potential pressure spikes.
Measurement and Control
Accurate measurement and control of hydraulic pressure are essential for system performance and safety. Modern hydraulic systems employ various types of pressure sensors and transducers to monitor hydraulic pressure continuously.
The study of hydrostatics and hydraulic pressure forms the foundation of fluid power technology. From the basic definition of hydraulic pressure as force per unit area to the complex applications in modern machinery, these principles guide the design and operation of countless hydraulic systems. Pascal's principle enables force multiplication and precise control, while the understanding of pressure distribution helps engineers create safe and efficient hydraulic components.
As technology advances, the fundamental principles of hydraulic pressure remain constant, continuing to provide reliable and powerful solutions for force transmission, motion control, and energy management in diverse applications. Whether in simple hydraulic jacks or sophisticated aerospace systems, the principles of hydraulic pressure serve as the cornerstone of fluid power engineering, demonstrating the enduring importance of understanding these fundamental concepts in liquid mechanics.